What we talk about when we talk about generalization?

Ultimately, generalization is the implicit alignment between neural networks and the underlying distribution \(p_{\mathrm{gt}}\) (i.e., human-defined data and perception).

Generalization as alignment. The network learns beyond the finite training set to approximate ground truth.

In diffusion models, this means generating realistic images not present in the training set, by learning a denoiser from empirical samples \(\bm{x}_{i=1\dots n}\). A standard training objective is:

\[\frac{1}{T}\sum_{t=0}^{T} \mathbb{E}_{\bm{x}\sim p_{\mathrm{gt}},\,\bm{\epsilon}\sim\mathcal{N}(\bm{0},\bm{I})} \!\left[\big\|\bm{f}_{\bm{\theta}}(\bm{x}+\sigma_t \bm{\epsilon},t)-\bm{x}\big\|^2\right].\]

If we learn a rich \(\bm{f}_{\bm{\theta}}(\bm{y}, t)\approx\bm{f}_{\mathrm{gt}}(\bm{y}, t)=\mathbb{E}\!\left[\bm{x} \mid \bm{x} + \sigma_t \bm{\epsilon} = \bm{y};\, \bm{x} \sim p_{\mathrm{gt}}\right]\) with this loss, sampling starts from noise and iteratively denoises into meaningful images, i.e., it generalizes.

However, this striking generalization ability is not simply due to neural networks’ ability to approximate arbitrary functions. Otherwise, training would routinely overfit to an empirical solution \(\bm{f}_{\mathrm{emp}}(\bm{y}, t)\) that memorizes training samples:

\[\bm{f}_{\mathrm{emp}}(\bm{y}, t) = \mathbb{E}\!\left[\bm{x}\mid \bm{x}+\sigma_t\bm{\epsilon}=\bm{y};\,\bm{x}\sim p_{\mathrm{emp}}\right] = \frac{\sum_{i=1}^n \mathcal{N}(\bm{y};\bm{x}_i,\sigma_t^2\bm{I})\,\bm{x}_i} {\sum_{i=1}^n \mathcal{N}(\bm{y};\bm{x}_i,\sigma_t^2\bm{I})}.\]

Understanding this requires looking into networks.

We study parameterized denoisers trained with gradient descent in a minimal setup: a two-layer ReLU network under a single noise level. Since it is also a denoising autoencoder, we call it ReLU-DAE.

\[\bm{f}_{\bm{W}_2,\bm{W}_1}(\bm{x}) = \bm{W}_2\bm{h}(\bm{x}) = \bm{W}_2\,[\bm{W}_1^\top \bm{x}]_+.\]

We prove a clean correspondence:
(i) memorization \(\Leftrightarrow\) \(\bm{W}_1, \bm{W}_2\) storing raw samples in the weights, approximating \(\bm{f}_{\mathrm{emp}}\);
(ii) generalization \(\Leftrightarrow\) \(\bm{W}_1, \bm{W}_2\) learning local data statistics, approximating \(\bm{f}_{\mathrm{gt}}\); and
(iii) a hybrid regime due to data imbalance.

Three regimes in ReLU-DAE learning. Memorization (left), hybrid (center), and generalization (right).

Representation learning follows naturally:

Memorized samples align perfectly with stored structures and produce spiky representations: think of a strong single-neuron response or retrieval of a specific training example.
Generalized samples align with a broader set of structures, yielding balanced representations that compose across neurons and reflect the underlying distribution, serving as coordinates for the image manifold.

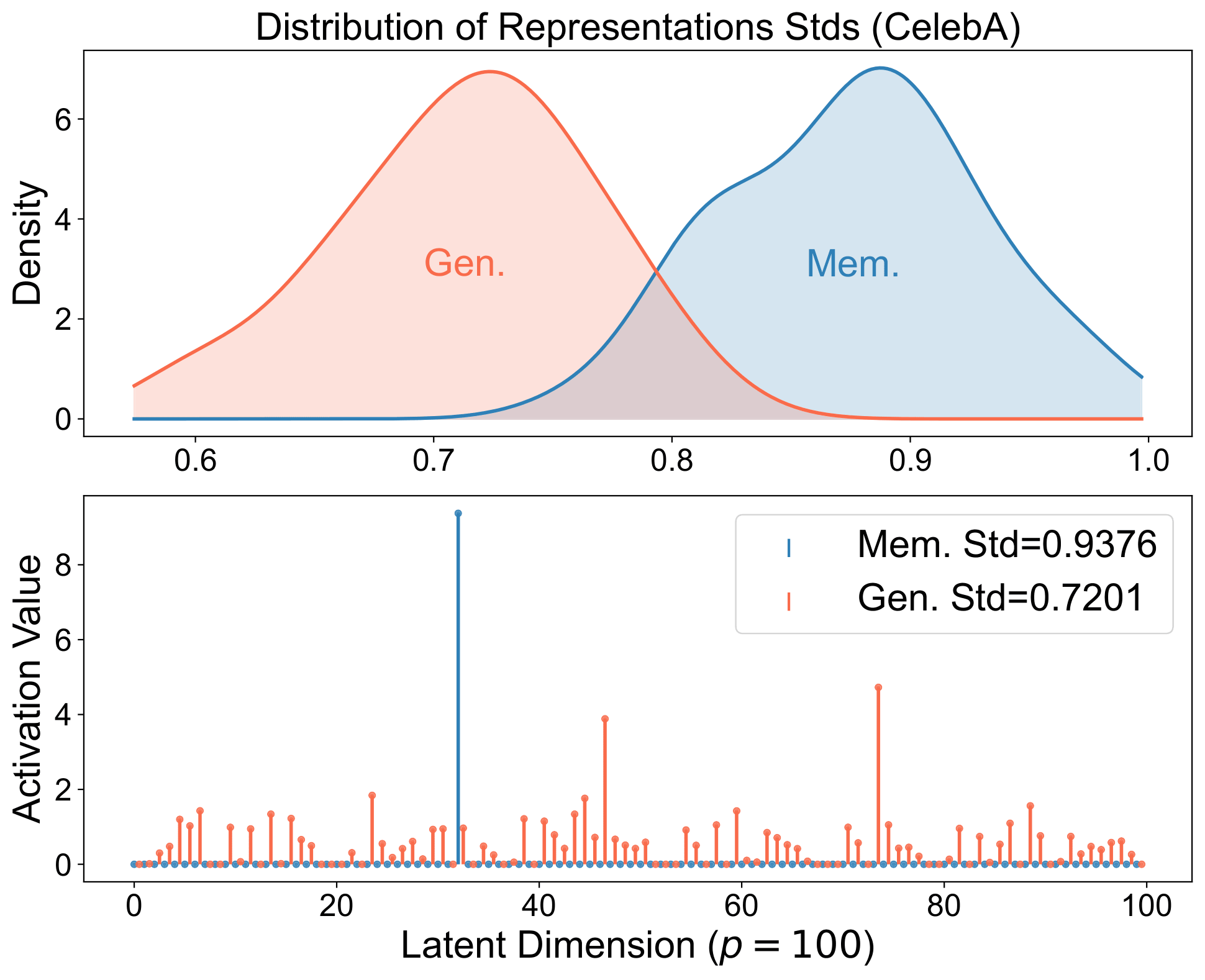
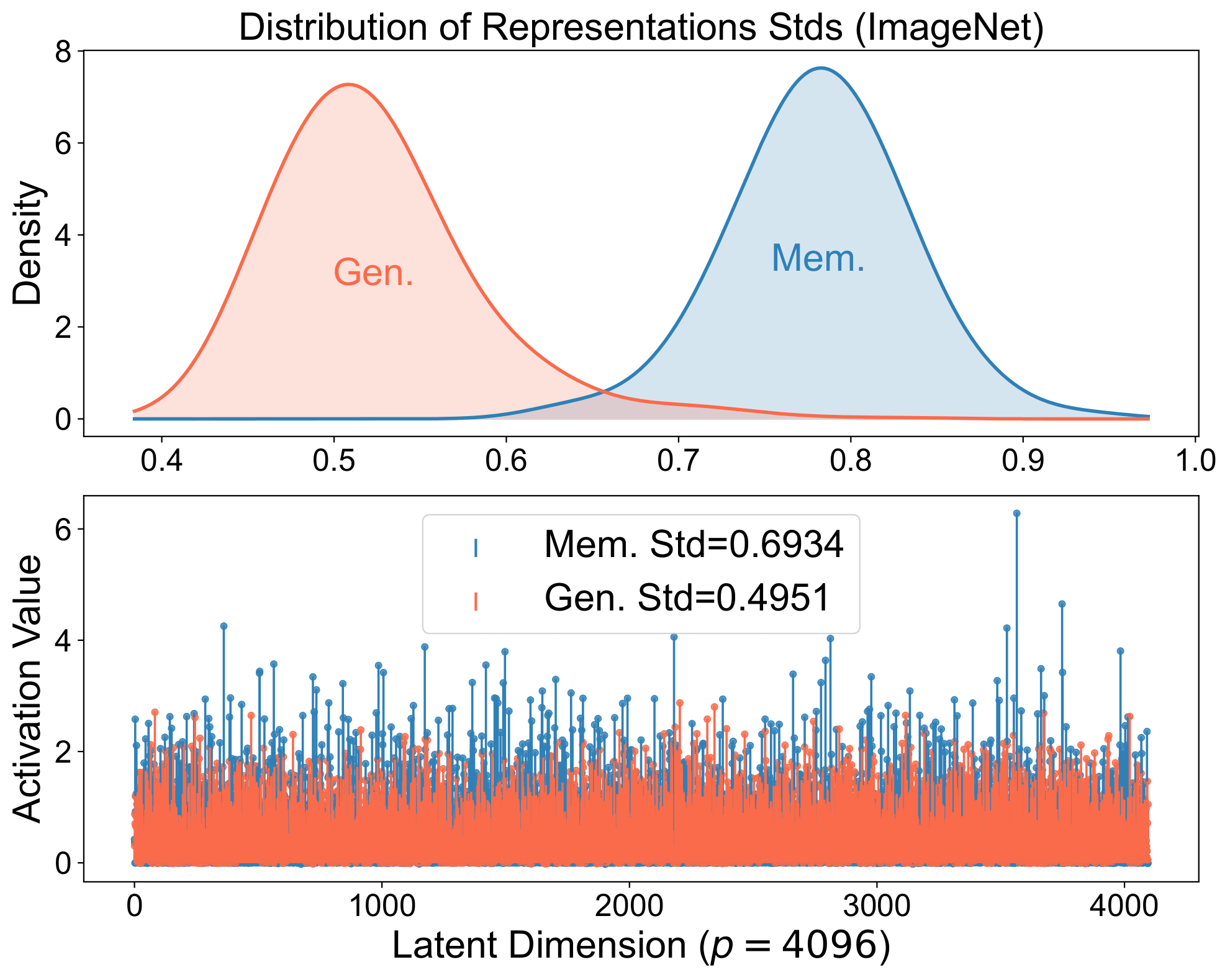
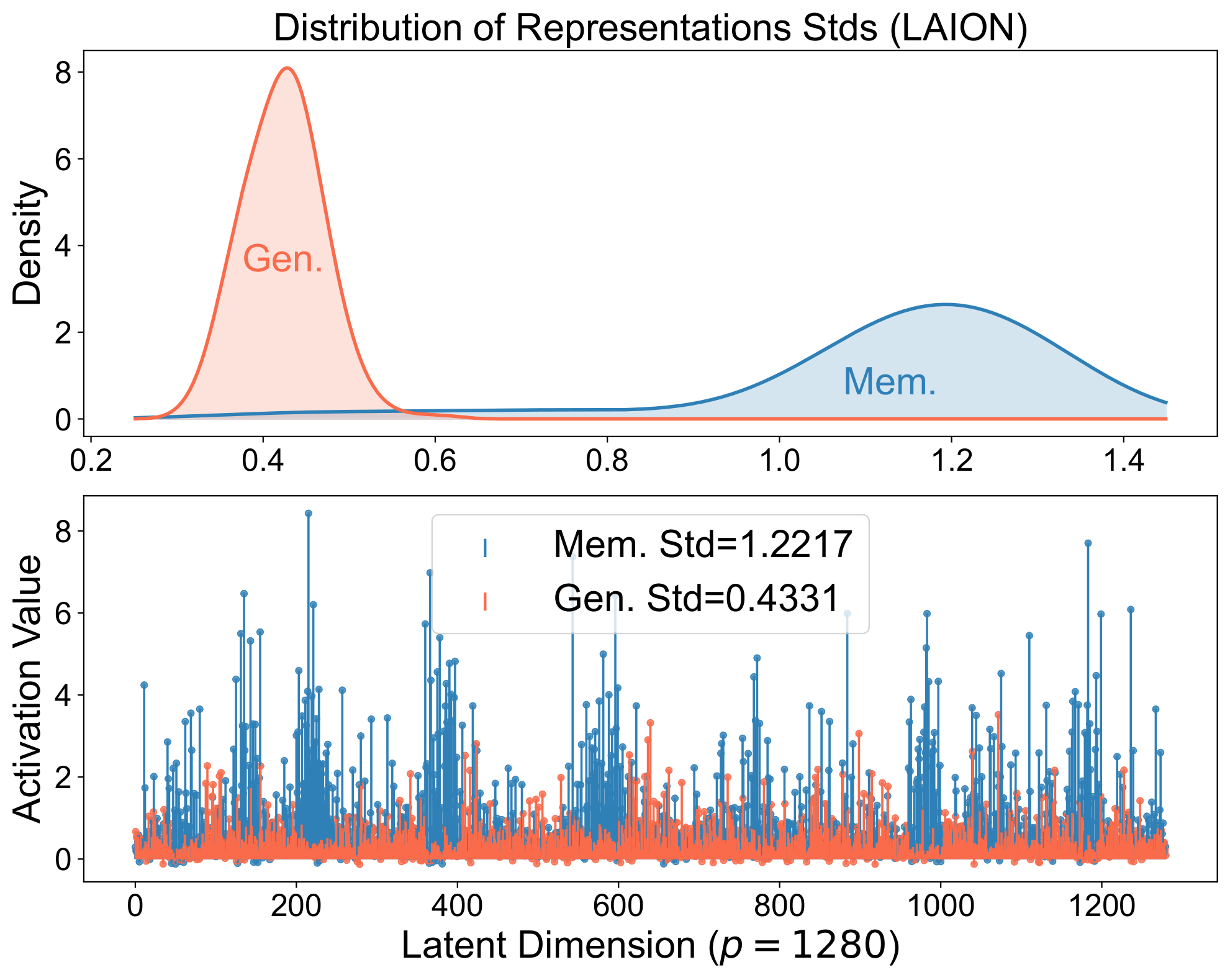
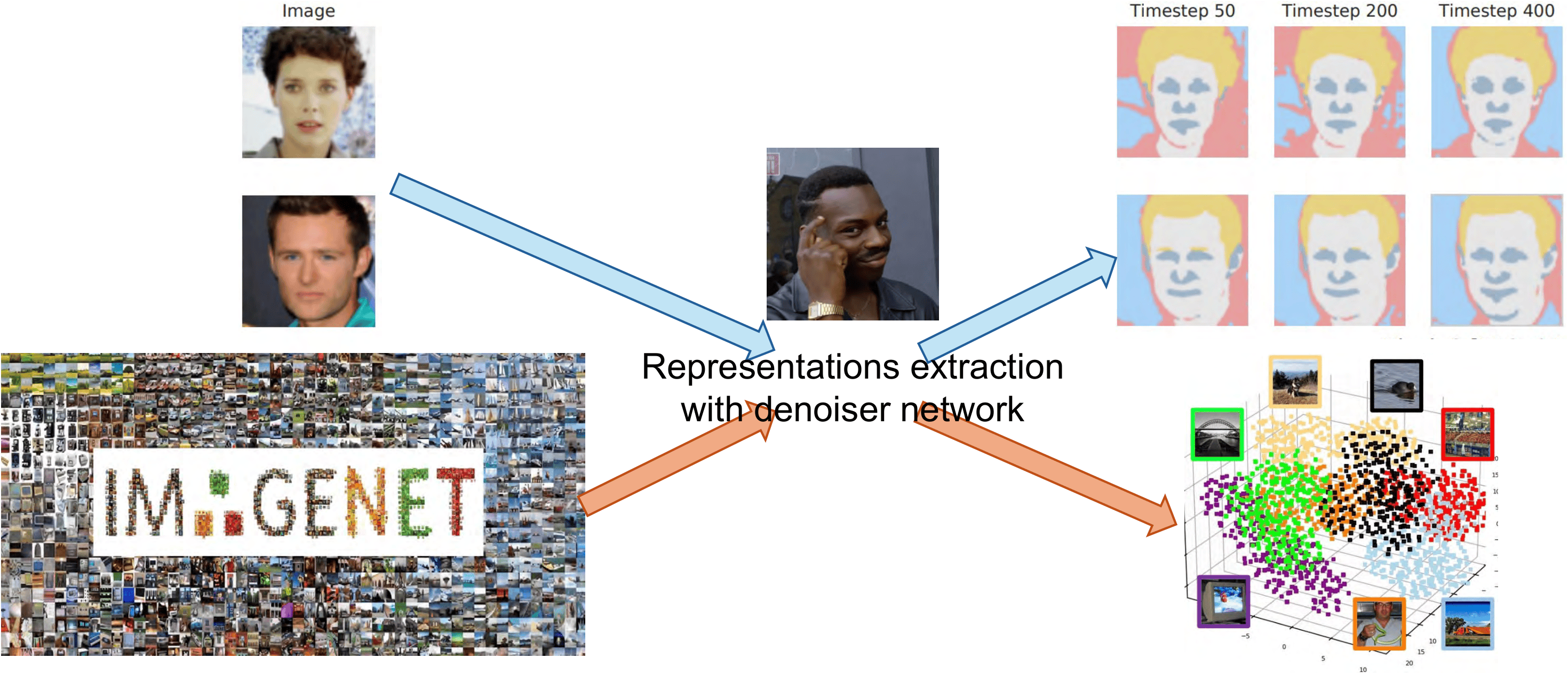
The same signature appears in real diffusion models. The spiky-vs-balanced separation persists in large models.

Generalized representations can also be manipulated to change the final output.

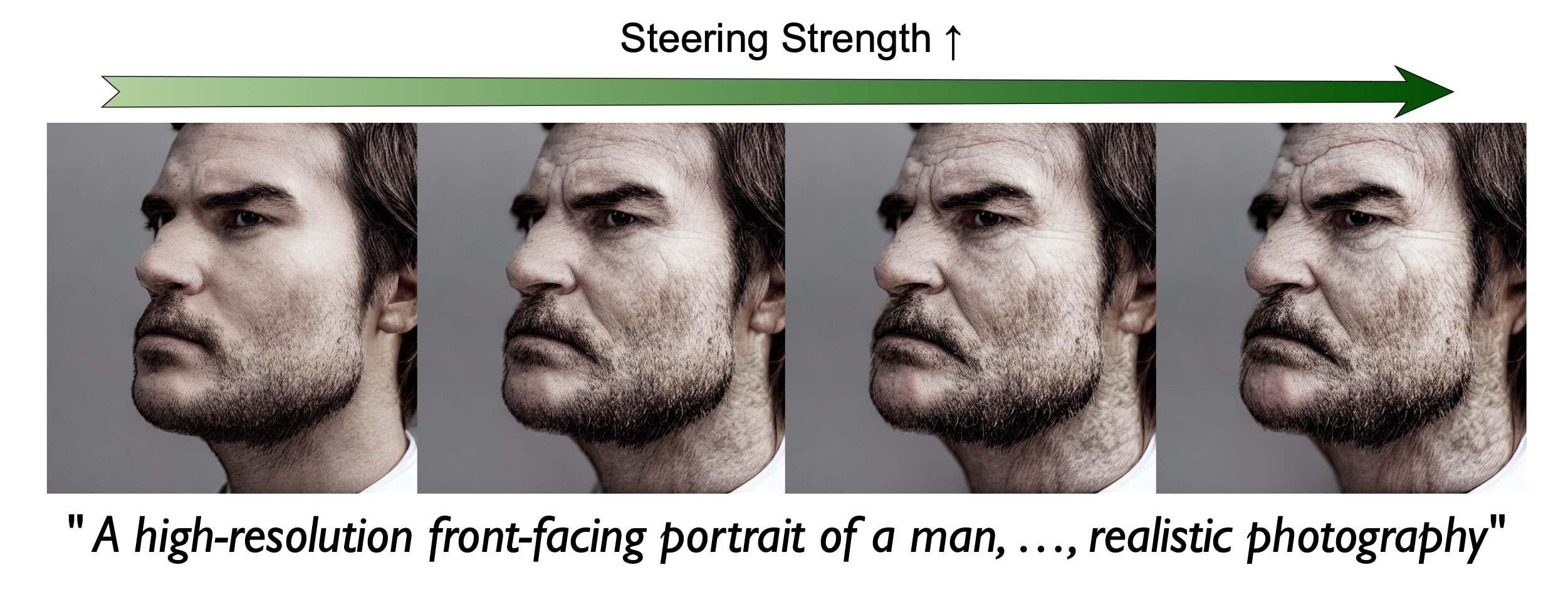
+Old (Gen.)

+Old (Mem.)

Image editing via representation steering. Works for generalized samples, but not for memorized samples.

Our theory starts from a simple two-layer network, but

we believe it reflects a fundamental mechanism in deep models: they project noisy inputs onto learned low-dimensional structure, arranging visually similar inputs into similar and meaningful activations (via ReLU gating in our theory).

This smart arrangement underlies their compression and denoising nature and aligns strongly with human perception. Internally, this is reflected as representation learning. Therefore, learning balanced and semantic representations is a strong indicator of generalization.